Formeln und Kalküle des isochoren Prozesses, tägliche Beispiele
AIsochore Prozess ist jeder Prozess des thermodynamischen Charakters, in dem das Volumen konstant bleibt. Diese Prozesse werden auch oft isometrisch oder isovolumen genannt. Im Allgemeinen kann ein thermodynamischer Prozess bei konstantem Druck stattfinden und wird dann als isobar bezeichnet.
Wenn es bei konstanter Temperatur auftritt, wird es in diesem Fall als isothermer Prozess bezeichnet. Wenn kein Wärmeaustausch zwischen dem System und der Umgebung stattfindet, sprechen wir über Adiabatik. Auf der anderen Seite, wenn es ein konstantes Volumen gibt, wird der erzeugte Prozess isochore genannt.

Im Fall des isochoren Prozesses kann bestätigt werden, dass in diesen Prozessen die Druck-Volumen-Arbeit Null ist, da dies aus der Multiplikation des Drucks mit der Zunahme des Volumens resultiert.
Darüber hinaus sind in einem thermodynamischen Druck-Volumen-Diagramm die isochoren Prozesse in Form einer vertikalen Geraden dargestellt.
Index
- 1 Formeln und Berechnung
- 1.1 Das erste Prinzip der Thermodynamik
- 1.2 Wärmekapazität bei konstantem Volumen
- 2 tägliche Beispiele
- 2.1 Der Otto-Idealzyklus
- 3 praktische Beispiele
- 3.1 Erstes Beispiel
- 3.2 Zweites Beispiel
- 4 Referenzen
Formeln und Berechnung
Das erste Prinzip der Thermodynamik
In der Thermodynamik berechnet sich die Arbeit aus folgendem Ausdruck:
W = P ΔV
In diesem Ausdruck ist W die in Joules gemessene Arbeit, P der Druck, der in Newton pro Quadratmeter gemessen wird, und ΔV ist die Veränderung oder Zunahme des Volumens, gemessen in Kubikmetern.
Gleiches gilt für das erste Prinzip der Thermodynamik:
Δ U = Q - W
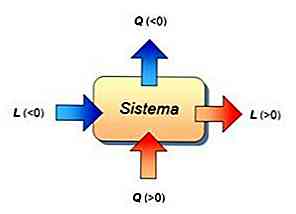
In dieser Formel ist W die durch das System oder das System geleistete Arbeit, Q ist die von dem System empfangene oder emittierte Wärme ΔU es ist die interne Energievariation des Systems. Bei dieser Gelegenheit werden die drei Größen in Joules gemessen.
Da die Arbeit in einem isochoren Prozess null ist, stellt sich heraus, dass es stimmt, dass:
Δ U = QV (da ΔV = 0 und daher W = 0)
Das heißt, die interne Energievariation des Systems beruht ausschließlich auf dem Austausch von Wärme zwischen dem System und der Umgebung. In diesem Fall wird die übertragene Wärme als Wärme bei konstantem Volumen bezeichnet.
 Wärmekapazität bei konstantem Volumen
Wärmekapazität bei konstantem Volumen
Die Wärmekapazität eines Körpers oder Systems ergibt sich aus der Aufteilung der Energiemenge in Form von Wärme, die in einem gegebenen Prozess auf einen Körper oder ein System übertragen wird, und der Temperaturänderung, die er erfährt.
Wenn der Prozess bei konstantem Volumen durchgeführt wird, wird die Wärmekapazität bei konstantem Volumen gesprochen und mit C bezeichnetv (molare Wärmekapazität)
Es wird in diesem Fall erfüllt sein:
Qv = n ∙ Cv ∙ ΔT
In einer solchen Situation ist n die Anzahl der Mole, Cv ist die zuvor erwähnte molare Wärmekapazität bei konstantem Volumen und ΔT ist die Temperaturerhöhung, die der Körper oder das System erfährt.
Tägliche Beispiele
Man kann sich leicht einen isochoren Prozess vorstellen, man muss nur an einen Prozess denken, der bei einem konstanten Volumen auftritt; das heißt, in dem der Behälter, der das Materie- oder Materialsystem enthält, sein Volumen nicht ändert.
Ein Beispiel könnte ein (ideales) Gas sein, das in einem geschlossenen Behälter eingeschlossen ist, dessen Volumen nicht durch irgendwelche Mittel geändert werden kann, denen Wärme zugeführt wird. Nehmen wir den Fall eines in einer Flasche eingeschlossenen Gases an.
Durch die Übertragung von Wärme auf das Gas, wie bereits erläutert, wird es zu einer Erhöhung oder Erhöhung seiner inneren Energie kommen.
Der umgekehrte Vorgang wäre der eines Gases, das in einem Behälter eingeschlossen ist, dessen Volumen nicht verändert werden kann. Wenn das Gas abkühlt und Wärme an die Umgebung abgibt, wird der Gasdruck verringert und der Wert der inneren Energie des Gases wird abnehmen.
Der Otto-Ideal-Zyklus
Der Otto-Zyklus ist ein idealer Fall des Zyklus, der von Benzinmotoren verwendet wird. Seine anfängliche Verwendung war jedoch in Maschinen, die Erdgas oder andere Brennstoffe in gasförmigem Zustand verwendeten.
In jedem Fall ist Ottos idealer Zyklus ein interessantes Beispiel für einen isochoren Prozess. Es tritt auf, wenn die Verbrennung des Benzin-Luft-Gemisches augenblicklich in einer Brennkraftmaschine stattfindet.
In diesem Fall findet eine Erhöhung der Temperatur und des Drucks des Gases innerhalb des Zylinders statt, wobei das Volumen konstant bleibt.
Praktische Beispiele
Erstes Beispiel
Gegeben ein (ideales) Gas, das in einem Zylinder mit einem Kolben eingeschlossen ist, geben Sie an, ob die folgenden Fälle Beispiele für isochore Prozesse sind.
- Eine 500 J Arbeit wird am Gas gemacht.
In diesem Fall wäre es kein isochore Prozess, da es für eine Arbeit am Gas notwendig ist, es zu komprimieren und daher sein Volumen zu verändern.
- Das Gas dehnt sich aus, indem es den Kolben horizontal verschiebt.
Wiederum wäre es kein isochore Prozess, da die Gasexpansion eine Variation ihres Volumens impliziert.
- Der Zylinderkolben ist so befestigt, dass er nicht verschoben werden kann und das Gas gekühlt wird.
Bei dieser Gelegenheit wäre es ein isochore Prozess, da es keine Volumenvariation geben würde.
Zweites Beispiel
Bestimmen Sie die Variation der inneren Energie, die von einem Gas in einem Behälter mit einem Volumen von 10 l bei 1 atm Druck erfahren wird, wenn seine Temperatur von 34ºC auf 60ºC in einem isochorischen Prozess, bekannt seine spezifische molare Hitze steigt Cv = 2.5·R (Sein R = 8,31 J / mol · K).
Da es sich um einen Prozess mit konstantem Volumen handelt, wird die Variation der inneren Energie nur als Folge der dem Gas zugeführten Wärme auftreten. Dies wird mit der folgenden Formel bestimmt:
Qv = n ∙ Cv ∙ ΔT
Um die zugeführte Wärme zu berechnen, müssen zunächst die im Behälter enthaltenen Gasmole berechnet werden. Dazu muss man auf die Gleichung der idealen Gase zurückgreifen:
P ∙ V = n ∙ R ∙ T
In dieser Gleichung ist n die Anzahl der Mole, R ist eine Konstante, deren Wert 8,31 J / mol · K ist, T ist die Temperatur, P ist der Druck, dem das Gas in Atmosphären ausgesetzt ist, und T ist die Temperatur gemessen in Kelvin.
Clear n und du bekommst:
n = R ∙ T / (P ∙ V) = 0,39 Mol
Also das:
Δ U = QV = n ∙ Cv ∙ ΔT = 0,39 ∙ 2,5 ∙ 8,31 ∙ 26 = 210,65 J
Referenzen
- Resnik, Halliday & Krane (2002).Physik Band 1. Cecsa.
- Laider, Keith, J. (1993). Oxford University Press, hrsg.Die Welt der Physikalischen Chemie.
- Wärmekapazität. (n. d.) In Wikipedia. Am 28. März 2018 von en.wikipedia.org abgerufen.
- Latente Hitze (n. d.) In Wikipedia. Am 28. März 2018 von en.wikipedia.org abgerufen.
- Isochore Prozess. (n. d.) In Wikipedia. Am 28. März 2018 von en.wikipedia.org abgerufen.



 Wärmekapazität bei konstantem Volumen
Wärmekapazität bei konstantem Volumen