Wie viele Kanten hat ein fünfeckiges Prisma?

Um zählen zu können Wie viele Kanten hat ein Pentagonalprisma?sind die Begriffe "Kante" (Kante eines Objekts), "Prisma" (geometrische Figur) und "pentagonal" (relativ zur Form einer geometrischen Figur) zu verstehen.

Wenn man über Pentagonal spricht, ist das erste, was man denken sollte, dass das Präfix "Penta" anzeigt, dass die Figur fünf Seiten haben muss. Daher muss die Figur eine Form haben, die der eines Pentagons ähnelt.

Eine "Kante" ist eine Kante eines Objekts. Geometrisch ist es eine Linie, die zwei aufeinanderfolgende Ecken einer geometrischen Figur verbindet.

Ein "Prisma" ist eine geometrische Figur, die durch zwei Basen begrenzt ist, die gleiche und parallele Polygone sind und deren Seitenflächen Parallelogramme sind.

In dem zu Beginn gezeigten Bild sind die Seitenflächen des fünfeckigen Prismas Rechtecke. Dies ist nur ein besonderer Fall, da die Definition angibt, dass die Seitenflächen Parallelogramme sind.

Dadurch können die Prismen als "gerade" und "schräg" klassifiziert werden.

Um zu wissen, wie viele Kanten ein fünfeckiges Prisma hat, spielt die Art des Prismas, mit der man arbeitet, keine Rolle. Sei es gerade oder schräg, die Anzahl der Kanten ändert sich nicht.

Möglichkeiten, die Kanten eines pentagonalen Prismas zu zählen

1- Erste Form

Da die Basen der fünfeckigen Prismen Fünfecke sind, hat jede Basis fünf Kanten.

Auf der anderen Seite wird von jedem Eckpunkt eines Fünfecks eine Kante auf den entsprechenden Eckpunkt des anderen Fünfecks projiziert; Das heißt, es gibt fünf Kanten, die eine Basis mit der anderen verbinden.

Durch Hinzufügen aller Kanten erhalten wir insgesamt 15 Kanten.

2. Zweite Form

Eine andere Art, die Kanten zu zählen, besteht darin, das fünfeckige Prisma in seinen zwei Basen und seinen Seitenflächen zu zerlegen. Dies ergibt zwei Fünfecke und ein Parallelogramm mit vier inneren Linien.

Jedes Fünfeck hat fünf Kanten. Auf der anderen Seite könnte man auf den ersten Blick den Fehler machen zu sagen, dass das Parallelogramm acht Kanten (sechs vertikale und zwei horizontale) enthält. Aber diese Argumentation sollte besser analysiert werden.

Wenn alle vertikalen Linien gezählt werden, ist es bemerkenswert, dass die erste Linie auf der linken Seite mit der letzten Linie auf der rechten Seite verbunden wird, wobei beide Linien eine einzelne Kante darstellen. Aber was ist mit den zwei horizontalen Linien?

Wenn alle Teile wieder zusammengesetzt sind, werden die horizontalen Linien jeweils mit den fünf Kanten jedes Fünfecks verbunden. Aus diesem Grund wäre das separate Zählen ein Fehler.

Das Parallelogramm enthält also fünf Kanten des Prismas, die zusammen mit den 10 am Anfang gezählten Kanten insgesamt 15 Kanten ergeben.

Andere Arten von Prismen

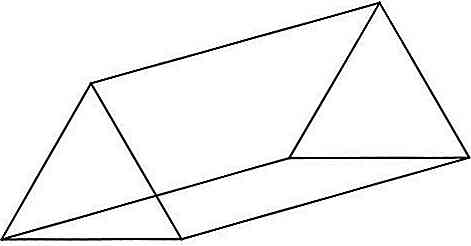
Dreiecksprisma

Dies sind Prismen, bei denen die Basen Dreiecke sind und die Anzahl der Kanten 9 beträgt.

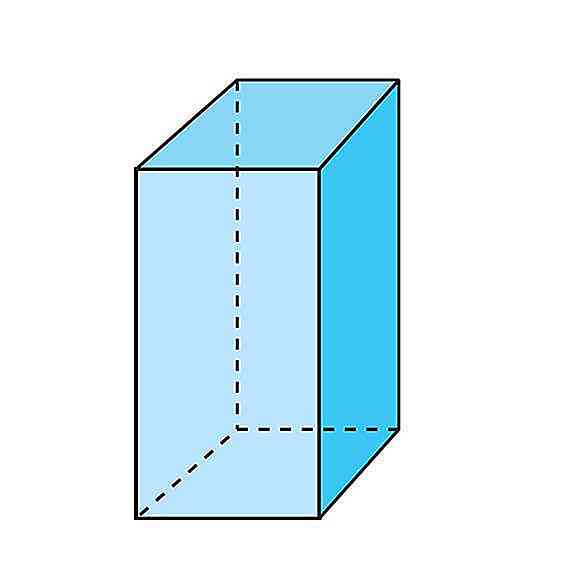
Viereckiges Prisma

Die Basen dieser Prismen sind Vierecke und die Anzahl der Kanten ist 12.

Sechseckiges Prisma

Die Basen sind Sechsecke und die Anzahl der Kanten ist 18.

Wie man an den anderen Arten von Prismen sehen kann, kann die Anzahl der Kanten durch eine mathematische Formel abgeleitet werden: sie wäre gleich 3 multipliziert mit der Anzahl der Seiten, die eine der Basen besitzt.

Wie bereits erwähnt, kann ein Prisma gerade oder schräg sein, aber zusätzlich gibt es regelmäßige und unregelmäßige Prismen sowie konvexe und konkave Prismen.

Referenzen

1. Billstein, R., Libeskind, S., und Lott, J. W. (2013). Mathematik: ein Problemlösungsansatz für Grundschullehrer. López Mateos Editores.
2. Fregoso, R. S. & Carrera, S. A. (2005). Mathematik 3. Fortschritt Editorial.
3. Gallardo, G. & Pilar, P. M. (2005). Mathematik 6. Fortschritt Editorial.
4. Gutiérrez, C. T. & Cisneros, M. P. (2005). Mathematikkurs 3. Fortschritt Editorial.
5. Kinsey, L., und Moore, T.E. (2006). Symmetrie, Form und Raum: Eine Einführung in die Mathematik durch Geometrie (illustriert, Nachdruck ed.). Springer Wissenschafts- und Wirtschaftsmedien.
6. Mitchell, C. (1999). Schillernde Math Line Designs (Illustrierte Ausgabe). Scholastic Inc.
7. R., M. P. (2005). Ich zeichne 6. Fortschritt Editorial.