Diskrete Mathematik, was sie dienen, Theorie der Mengen

Die diskrete Mathematik entsprechen einem Bereich der Mathematik, der für das Studium der Menge natürlicher Zahlen verantwortlich ist; das heißt, die Menge der endlichen und unendlichen zählbaren Zahlen, bei denen die Elemente nacheinander einzeln gezählt werden können.

Diese Mengen sind als diskrete Mengen bekannt; Ein Beispiel für diese Mengen sind ganze Zahlen, Graphen oder logische Ausdrücke, und sie werden in verschiedenen Bereichen der Wissenschaft, hauptsächlich in der Informatik oder Computertechnik, angewendet.

Index

• 1 Beschreibung
• 2 Was bringt die diskrete Mathematik?
  • 2.1 Kombinatorisches
  • 2.2 Theorie der diskreten Verteilung
  • 2.3 Informationstheorie
  • 2.4 Rechnen
  • 2.5 Kryptographie
  • 2.6 Logik
  • 2.7 Theorie der Graphen
  • 2.8 Algebra
  • 2.9 Geometrie
• 3 Theorie der Mengen
  • 3.1 Endlicher Satz
  • 3.2 Unendliche Buchführung
• 4 Diskretisierung
• 5 Referenzen

Beschreibung

In der diskreten Mathematik sind Prozesse zählbar, basierend auf ganzen Zahlen. Dies bedeutet, dass Dezimalzahlen nicht verwendet werden und daher die Approximation oder die Grenzen nicht wie in anderen Bereichen verwendet werden. Zum Beispiel kann eine Unbekannte gleich 5 oder 6 sein, aber niemals 4,99 oder 5,9.

Auf der anderen Seite sind die Variablen in der graphischen Darstellung diskret und werden von einer endlichen Menge von Punkten gegeben, die einzeln gezählt werden, wie im Bild zu sehen ist:

Die diskrete Mathematik entsteht durch die Notwendigkeit, eine genaue Studie zu erhalten, die kombiniert und getestet werden kann, um sie in verschiedenen Bereichen anzuwenden.

Was nutzt die diskrete Mathematik?

Diskrete Mathematik wird in mehreren Bereichen verwendet. Unter den wichtigsten sind die folgenden:

Kombinatorisch

Studiere endliche Mengen, in denen Elemente geordnet oder kombiniert und gezählt werden können.

Theorie der diskreten Verteilung

Studieren Sie Ereignisse, die in Räumen auftreten, in denen Samples gezählt werden können, in denen kontinuierliche Verteilungen verwendet werden, um diskrete Verteilungen zu approximieren, oder umgekehrt.

Informationstheorie

Es bezieht sich auf die Codierung von Informationen, die für den Entwurf und die Übertragung und Speicherung von Daten verwendet werden, wie beispielsweise analoge Signale.

IT

Durch diskrete Mathematik werden Probleme mit Hilfe von Algorithmen gelöst, und es wird untersucht, was berechnet werden kann und wie viel Zeit dafür benötigt wird (Komplexität).

Die Bedeutung der diskreten Mathematik in diesem Bereich hat in den letzten Jahrzehnten zugenommen, insbesondere für die Entwicklung von Programmiersprachen und Software.

Kryptographie

Es basiert auf diskreter Mathematik, um Sicherheitsstrukturen oder Verschlüsselungsmethoden zu erstellen. Ein Beispiel für diese Anwendung sind die Passwörter, die getrennt Bits senden, die Informationen enthalten.

Durch die Untersuchung können die Eigenschaften von ganzen Zahlen und Primzahlen (Zahlentheorie) diese Sicherheitsmethoden erzeugen oder zerstören.

Logik

Es werden diskrete Strukturen verwendet, die üblicherweise eine endliche Menge bilden, um Sätze zu beweisen oder beispielsweise Software zu verifizieren.

Graphentheorie

Es ermöglicht die Auflösung logischer Probleme mit Knoten und Linien, die eine Art von Graphen bilden, wie in der folgenden Abbildung gezeigt:

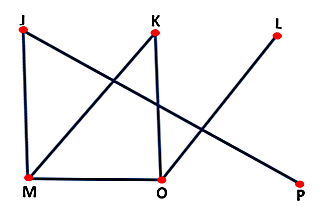Algebra

Es ist ein Bereich, der eng mit der diskreten Mathematik verbunden ist, weil die algebraischen Ausdrücke diskret sind. Dadurch werden elektronische Schaltungen, Prozessoren, Programmierung (Boolesche Algebra) und Datenbanken (relationale Algebra) entwickelt.

Geometrie

Studieren Sie die kombinatorischen Eigenschaften von geometrischen Objekten, wie z. B. die Beschichtung der Ebene. Auf der anderen Seite ermöglicht die computergestützte Geometrie die Entwicklung geometrischer Probleme durch Anwendung von Algorithmen.

Theorie der Sätze

In diskreten mathematischen Mengen (endliche und unendliche Zahl) sind die Hauptziele der Studie. Die Theorie der Mengen wurde von George Cantor veröffentlicht, der zeigte, dass alle unendlichen Mengen die gleiche Größe haben.

Ein Set ist eine Gruppierung von Elementen (Zahlen, Dinge, Tiere und Menschen, ua), die gut definiert sind; das heißt, es gibt eine Beziehung, nach der jedes Element zu einer Menge gehört, und wird beispielsweise ausgedrückt als ∈ A.

In der Mathematik gibt es verschiedene Mengen, die bestimmte Zahlen nach ihren Eigenschaften gruppieren. So haben Sie zum Beispiel:

- Menge natürlicher Zahlen N = {0, 1, 2, 3, 4, 5, 6, ... + ∞}.

- Satz von ganzen Zahlen E = {-∞ ..., -3, -2, -1, 0, 1, 2, 3, ... + ∞}.

- Teilmenge der rationalen Zahlen Q * = {-∞ ..., - ¼, - ½, 0, ¼, ½, ... ∞}.

- Menge reeller Zahlen R = {-∞ ..., - ½, -1, 0, ½, 1, ... ∞}.

Die Sätze sind mit Buchstaben des Alphabets in Großbuchstaben benannt; während die Elemente in Kleinbuchstaben, in geschweiften Klammern ({}) benannt und durch Kommas getrennt sind (,). Sie werden normalerweise in Diagrammen wie Venns und Carolls sowie rechnerisch dargestellt.

Mit grundlegenden Operationen wie Vereinigungs-, Schnittpunkt-, Komplement-, Differenz- und kartesischem Produkt werden die Mengen und ihre Elemente basierend auf dem Zugehörigkeitsverhältnis verwaltet.

Es gibt verschiedene Arten von Mengen, die in der diskreten Mathematik am häufigsten untersucht werden:

Endgültiger Satz

Es ist eine, die eine endliche Anzahl von Elementen hat und die einer natürlichen Zahl entspricht. So ist zum Beispiel A = {1, 2, 3,4} eine endliche Menge, die 4 Elemente hat.

Unendliche Buchführung

Es ist derjenige, in dem eine Entsprechung zwischen den Elementen einer Menge und den natürlichen Zahlen besteht; das heißt, dass aus einem Element alle Elemente eines Satzes nacheinander aufgelistet werden können.

Auf diese Weise entspricht jedes Element jedem Element der Menge natürlicher Zahlen. Zum Beispiel:

Die Menge der ganzen Zahlen Z = {... -2, -1, 0, 1, 2 ...} kann als Z = {0, 1, -1, 2, -2 ...} aufgeführt werden. Auf diese Weise ist es möglich, eine Eins-zu-eins-Entsprechung zwischen den Elementen von Z und den natürlichen Zahlen herzustellen, wie in der folgenden Abbildung gezeigt:

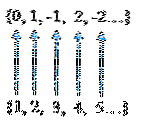Diskretisierung

Es ist eine Methode, um kontinuierliche Probleme (Modelle und Gleichungen) zu lösen, die in diskrete Probleme umgewandelt werden müssen, in denen die Lösung mit der Annäherung der Lösung des kontinuierlichen Problems bekannt ist.

Mit anderen Worten, die Diskretisierung versucht, aus einer unendlichen Menge von Punkten eine endliche Quantität zu extrahieren; Auf diese Weise wird eine kontinuierliche Einheit in einzelne Einheiten umgewandelt.

Im Allgemeinen wird diese Methode in der numerischen Analyse verwendet, wie zum Beispiel bei der Lösung einer Differentialgleichung, mittels einer Funktion, die durch eine endliche Menge von Daten in ihrer Domäne dargestellt wird, selbst wenn sie kontinuierlich ist.

Ein weiteres Beispiel für die Diskretisierung ist die Verwendung eines analogen Signals in ein digitales Signal, wenn kontinuierliche Signaleinheiten in einzelne Einheiten umgewandelt (diskretisiert) und dann codiert und quantisiert werden, um ein digitales Signal zu erhalten.

Referenzen

1. Grimaldi, R. P. (1997). Diskrete und kombinatorische Mathematik. Addison Wesley Iberoamericana.
2. Ferrando, V. Gregori. (1995). Diskrete Mathematik Reverte
3. Jech, T. (2011). Set-Theorie. Stanford Enzyklopädie der Philosophie.
4. José Francisco Villalpando Becerra, A. G. (2014). Diskrete Mathematik: Anwendungen und Übungen. Grupo Redaktion Patria.
5. Landau, R. (2005). Computing, ein erster Kurs in wissenschaftlichen.
6. Merayo, F.G. (2005). Diskrete Mathematik. Thomson Redaktion.
7. Rosen, K. H. (2003). Diskrete Mathematik und ihre Anwendungen. McGraw-Hügel.
8. Schneider, D. G. (1995). Ein logischer Ansatz für Diskrete Mathematik.