Gesetze der Exponenten (mit aufgelösten Beispielen und Übungen)
Die Gesetze von Exponenten sind diejenigen, die für diese Zahl gelten, die angibt, wie oft eine Basennummer mit sich selbst multipliziert werden muss. Die Exponenten werden auch als Potenzen bezeichnet. Die Potenzierung ist eine mathematische Operation, die durch eine Basis (a), den Exponenten (m) und die Potenz (b) gebildet wird, die das Ergebnis der Operation ist.
Exponenten werden im Allgemeinen verwendet, wenn sehr große Mengen verwendet werden, weil diese nicht mehr als Abkürzungen sind, die die Multiplikation derselben Nummer eine bestimmte Anzahl von Malen darstellen. Die Exponenten können sowohl positiv als auch negativ sein.

Index
- 1 Erklärung der Gesetze der Exponenten
- 1.1 Erstes Gesetz: Exponentenstärke gleich 1
- 1.2 Zweites Gesetz: Exponentenstärke gleich 0
- 1.3 Drittes Gesetz: negativer Exponent
- 1.4 Viertes Gesetz: Multiplikation von Mächten mit gleicher Basis
- 1.5 Fünftes Gesetz: Gewaltenteilung mit gleicher Basis
- 1.6 Sechstes Gesetz: Multiplikation von Mächten mit einer anderen Basis
- 1.7 Siebentes Gesetz: Gewaltenteilung mit einer anderen Basis
- 1.8 Achtes Gesetz: Macht einer Macht
- 1.9 Neuntes Gesetz: Teilexponent
- 2 Übungen gelöst
- 2.1 Aufgabe 1
- 2.2 Aufgabe 2
- 3 Referenzen
Erklärung der Gesetze der Exponenten
Wie oben erwähnt, sind Exponenten eine abgekürzte Form, die die Multiplikation von Zahlen an sich mehrmals darstellt, wobei der Exponent nur mit der Zahl links zusammenhängt. Zum Beispiel:
23 = 2*2*2 = 8
In diesem Fall ist die Zahl 2 die Basis der Potenz, die 3 Mal multipliziert wird, wie durch den Exponenten in der oberen rechten Ecke der Basis angegeben. Es gibt verschiedene Arten den Ausdruck zu lesen: 2 erhöht auf 3 oder auch 2 erhöht auf den Würfel.
Exponenten geben auch an, wie oft sie geteilt werden können, und um diese Operation von der Multiplikation zu unterscheiden, trägt der Exponent das Minuszeichen (-) davor (es ist negativ), was bedeutet, dass der Exponent im Nenner von a steht Fraktion. Zum Beispiel:
2- 4 = 1/ 2*2*2*2 = 1/16
Dies sollte nicht mit dem Fall verwechselt werden, in dem die Basis negativ ist, da es davon abhängt, ob der Exponent gerade oder ungerade ist, um zu bestimmen, ob die Potenz positiv oder negativ ist. Also musst du:
- Wenn der Exponent gerade ist, wird die Leistung positiv sein. Zum Beispiel:
(-7)2 = -7 * -7 = 49.
- Wenn der Exponent ungerade ist, wird die Leistung negativ sein. Zum Beispiel:
(-2)5 = (-2)*(-2)*(-2)*(-2)*(-2)=-32.
Es gibt einen speziellen Fall, in dem, wenn der Exponent gleich 0 ist, die Potenz gleich 1 ist. Es besteht auch die Möglichkeit, dass die Basis 0 ist; In diesem Fall wird die Leistung in Abhängigkeit von der Belichtung unbestimmt sein oder nicht.
Um mathematische Operationen mit den Exponenten auszuführen, müssen einige Regeln oder Regeln befolgt werden, die es einfacher machen, die Lösung für diese Operationen zu finden.
Erstes Gesetz: Exponentenstärke gleich 1
Wenn der Exponent 1 ist, ist das Ergebnis der gleiche Wert der Basis: a1 = a.
Beispiele
91 = 9.
221 = 22.
8951 = 895.
Zweites Gesetz: Exponentenstärke gleich 0
Wenn der Exponent 0 ist und die Basis ungleich Null ist, lautet das Ergebnis :, a0 = 1.
Beispiele
10 = 1.
3230=1.
10950 = 1.
Drittes Gesetz: negativer Exponent
Da die Exponate negativ sind, wird das Ergebnis ein Bruch sein, wobei die Stärke der Nenner sein wird. Wenn zum Beispiel m positiv ist, dann a-m= 1 / am.
Beispiele
- 3-1 = 1/ 3.
- 6-2 = 1 / 62 = 1/36.
- 8-3 = 1/ 83 = 1/512.
Viertes Gesetz: Multiplikation der Kräfte mit gleicher Basis
Um Potenzen zu multiplizieren, wo die Basen gleich sind und sich von 0 unterscheiden, wird die Basis beibehalten und die Exponenten werden hinzugefügt: am * an = am + n.
Beispiele
- 44 * 43 = 44+3 = 47
- 81 * 84 = 81+4 = 85
- 22 * 29 = 22+9 = 211
Fünftes Gesetz: Gewaltenteilung mit gleicher Basis
Um Potenzen zu teilen, in denen die Basen gleich und verschieden von 0 sind, wird die Basis beibehalten und die Exponenten wie folgt subtrahiert: am / an = am-n.
Beispiele
- 92 / 91 = 9 (2 - 1) = 91.
- 615 / 610 = 6 (15 - 10) = 65.
- 4912 / 496 = 49 (12 - 6) = 496.
Sechstes Gesetz: Multiplikation von Mächten mit einer anderen Basis
In diesem Gesetz haben wir das Gegenteil von dem, was im vierten ausgedrückt ist; Das heißt, wenn es verschiedene Basen mit gleichen Exponenten gibt, werden die Basen multipliziert und der Exponent wird beibehalten: am * bm = (a*b) m.
Beispiele
- 102 * 202 = (10 * 20)2 = 2002.
- 4511 * 911 = (45*9)11 = 40511.
Eine andere Möglichkeit, dieses Gesetz zu repräsentieren, ist, wenn eine Multiplikation zu einer Potenz erhoben wird. Somit wird der Exponent zu jedem der Terme gehören: (a*b)m= am* bm.
Beispiele
- (5*8)4 = 54 * 84 = 404.
- (23 * 7)6 = 236 * 76 = 1616.
Siebentes Gesetz: Gewaltenteilung mit unterschiedlicher Basis
Wenn es verschiedene Basen mit gleichen Exponenten gibt, werden die Basen geteilt und der Exponent beibehalten: am / bm = (a / b)m.
Beispiele
- 303 / 23 = (30/2)3 = 153.
- 4404 / 804 = (440/80)4 = 5,54.
Wenn eine Division zu einer Potenz erhoben wird, gehört der Exponent zu jedem der Terme: (a / b) m = am / bm.
Beispiele
- (8/4)8 = 88 / 48 = 28.
- (25/5)2 = 252 / 52 = 52.
Es gibt einen Fall, in dem der Exponent negativ ist. Um also positiv zu sein, wird der Wert des Zählers wie folgt mit dem des Nenners invertiert:
- (a / b)-n = (b / a)n = bn / an.
- (4/5) -9 = ( 5 / 4) 9 = 59 / 44.
Achtes Gesetz: Macht einer Macht
Wenn Sie eine Potenz haben, die auf eine andere Potenz - also zwei Exponenten gleichzeitig - erhöht wird, wird die Basis beibehalten und die Exponenten multiplizieren: (am)n= am *n.
Beispiele
- (83)2 = 8 (3*2) = 86.
- (139)3 = 13 (9*3) = 1327.
- (23810)12 = 238(10 * 12) = 238120.
Neuntes Gesetz: Teilexponent
Wenn die Potenz einen Bruch als Exponent hat, wird sie durch Transformation in eine n-te Wurzel aufgelöst, wobei der Zähler als Exponent und der Nenner den Index der Wurzel darstellt:
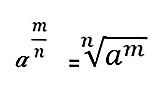 Beispiel
Beispiel

Gelöste Übungen
Übung 1
Berechnen Sie die Operationen zwischen den Potenzen, die unterschiedliche Basen haben:
24 * 44 / 82.
Lösung
Mit den Regeln der Exponenten werden im Zähler die Basen multipliziert und der Exponent beibehalten, so:
24 * 44 / 82=(2*4)4 / 82 = 84 / 82
Nun, da wir die gleichen Basen haben, aber unterschiedliche Exponenten haben, wird die Basis beibehalten und die Exponenten subtrahiert:
84 / 82 = 8(4 - 2) = 82
Übung 2
Berechnen Sie die Operationen zwischen den hohen Kräften zu einer anderen Macht:
(32)3 * (2 * 65)-2 * (22)3
Lösung
Bei der Anwendung der Gesetze müssen Sie:
(32)3 * (2 * 65)-2 * (22)3
=36 * 2-2 * 2-10 * 26
=36 * 2(-2) + (- 10) * 26
=36 * 2-12 * 26
=36 * 2(-12) + (6)
=36 * 26
=(3*2)6
=66
=46.656
Referenzen
- Aponte, G. (1998). Grundlagen der Grundlegenden Mathematik. Pearson Ausbildung.
- Corbalán, F. (1997). Mathematik im täglichen Leben angewendet.
- Jiménez, J. R. (2009). Mathematik 1 SEP.
- Max Peters, W. L. (1972). Algebra und Trigonometrie
- Rees, P.K. (1986). Reverte



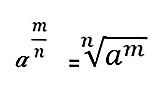 Beispiel
Beispiel