Satz von Thales von Milet Erster, Zweiter und Beispiele

Der erste und der zweite Theorem von Thales von Miletus sie basieren auf der Bestimmung von Dreiecken aus anderen ähnlichen (erster Satz) oder Umfängen (zweiter Satz). Sie waren in verschiedenen Bereichen sehr nützlich. Zum Beispiel erwies sich der erste Satz als sehr nützlich für die Messung großer Strukturen, wenn es keine ausgefeilten Messinstrumente gab.

Thales von Milet war ein griechischer Mathematiker, der große Beiträge zur Geometrie lieferte, von der diese beiden Theoreme hervorstechen (in manchen Texten schreiben sie auch als Thales), und ihre nützlichen Anwendungen. Diese Ergebnisse wurden im Laufe der Geschichte verwendet und ermöglichten die Lösung einer Vielzahl geometrischer Probleme.

Index

• 1 Erster Theorem der Geschichten
  • 1.1 Anwendung
  • 1.2 Beispiele
• 2 Zweiter Satz der Geschichten
  • 2.1 Anwendung
  • 2.2 Beispiel
• 3 Referenzen

Erster Satz von Tales

Das erste Theorem von Tales ist ein sehr nützliches Werkzeug, das unter anderem erlaubt, ein Dreieck ähnlich einem anderen, vorher bekannt zu bauen. Daraus leiten sich verschiedene Versionen des Theorems ab, die in mehreren Kontexten angewendet werden können.

Bevor Sie Ihre Aussage machen, erinnern Sie sich an einige Begriffe der Ähnlichkeit von Dreiecken. Im Wesentlichen sind zwei Dreiecke ähnlich, wenn ihre Winkel kongruent sind (sie haben das gleiche Maß). Dies führt dazu, dass, wenn zwei Dreiecke ähnlich sind, ihre entsprechenden Seiten (oder Homologen) proportional sind.

Der erste Satz von Thales besagt, dass, wenn in einem gegebenen Dreieck eine gerade Linie parallel zu irgendeiner seiner Seiten gezeichnet wird, das neue Dreieck, das erhalten wird, dem Anfangsdreieck ähnlich ist.

In der vorherigen Abbildung sind die Dreiecke ABC und DEC ähnlich. Die Proportionalität, die aufgrund dieser Ähnlichkeit erhalten wird, führt auch zu einer Proportionalitätsbeziehung zwischen zwei Seiten des gleichen Dreiecks und den zwei entsprechenden Seiten des anderen. Zum Beispiel müssten Sie unter Berücksichtigung der vorherigen Zahlen auch:Ein anderer Weg, auf dem Sie den ersten Satz von Thales sehen können, und der auch sehr nützlich ist, ist folgender: Wenn zwei Linien L1 und L2 (any) durch parallele Linien (irgendeine Anzahl von diesen) geschnitten werden, dann die Segmente in L1 gebildet sind proportional zu den entsprechenden in L2 gebildet.

Sie erhalten auch eine Beziehung zwischen den gebildeten Winkeln, wie in der folgenden Abbildung zu sehen ist.

Anwendung

Unter seinen vielfältigen Anwendungen sticht eines von besonderem Interesse hervor und hat mit einer der Arten zu tun, in denen große Strukturen in der Antike gemessen wurden, in der Zeit, in der Thales lebte und in denen die modernen Messgeräte nicht verfügbar waren. Sie existieren jetzt.

Man sagt, dass Thales so die höchste Pyramide in Ägypten, Cheops, messen konnte. Thales vermutete dabei, dass die Reflexionen der Sonnenstrahlen den Boden berührten und parallele Linien bildeten. Unter dieser Annahme steckte er einen Stab oder Stock vertikal in den Boden.

Dann benutzte er die Ähnlichkeit der zwei sich ergebenden Dreiecke, von denen eines durch die Länge des Schattens der Pyramide (die leicht berechnet werden kann) und die Höhe der Pyramide (das Unbekannte) und das andere durch die Längen des Schattens gebildet wurde und die Höhe der Stange (die auch leicht berechnet werden kann).

Unter Verwendung der Proportionalität zwischen diesen Längen können Sie die Höhe der Pyramide löschen und kennen.

Obwohl diese Messmethode einen signifikanten Näherungsfehler in Bezug auf die Genauigkeit der Höhe ergeben kann und von der Parallelität der Sonnenstrahlen abhängt (was wiederum von einer genauen Zeit abhängt), müssen wir erkennen, dass es eine sehr geniale Idee ist und das bot eine gute Alternative zur Messung für die Zeit.

Beispiele

Finde den Wert von x in jedem Fall:

Erster Fall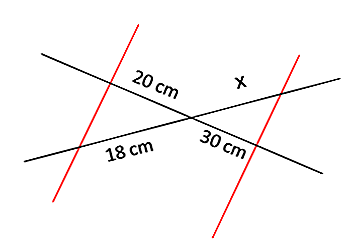 

Lösung

Hier haben wir zwei Linien, die durch zwei parallele Linien geschnitten sind. Nach dem ersten Satz von Thales hat man, dass ihre jeweiligen Seiten proportional sind. Insbesondere:

Zweiter Fall

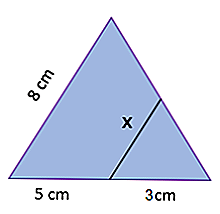
Lösung

Hier haben wir zwei Dreiecke, von denen eines durch ein Segment parallel zu einer der Seiten des anderen (genau die Seite der Länge x) gebildet wird. Nach dem ersten Theorem von Tales musst du:

Zweiter Satz von Geschichten

Der zweite Satz von Thales bestimmt ein rechtwinkliges Dreieck, das an jedem Punkt desselben in einen Umfang eingeschrieben ist.

Ein Dreieck, das einem Umfang zugeordnet ist, ist ein Dreieck, dessen Ecken auf dem Umfang liegen und somit in diesem enthalten sind.

Insbesondere besagt der zweite Satz von Thales Folgendes: Bei einem Kreis aus Mittelpunkt O und Durchmesser AC bestimmt jeder Punkt B des Umfangs (außer A und C) ein rechtes Dreieck ABC mit rechtem Winkel <>

Als Begründung sei angemerkt, dass sowohl OA als auch OB und OC dem Radius des Umfangs entsprechen; Daher sind ihre Messungen die gleichen. Von dort wird erreicht, dass die Dreiecke OAB und OCB gleichschenklig sind, wobei

Es ist bekannt, dass die Summe der Winkel eines Dreiecks gleich 180º ist. Mit diesem Dreieck ABC müssen Sie:

2b + 2a = 180º.

Äquivalenz haben wir, dass b + a = 90º und b + a =

Beachten Sie, dass das rechte Thales-zweite Theorem genau das ist, dessen Hypotenuse gleich dem Durchmesser des Umfangs ist.Daher wird es vollständig durch den Halbkreis bestimmt, der die Punkte des Dreiecks enthält; in diesem Fall der obere Halbkreis.

Man beachte auch, dass in dem rechtwinkligen Dreieck, das mittels des zweiten Satzes von Thales erhalten wird, die Hypotenuse durch OA und OC (den Radius) in zwei gleiche Teile geteilt wird. Dieses Maß ist wiederum gleich dem Segment OB (auch der Radius), das dem Median des Dreiecks ABC von B entspricht.

Mit anderen Worten, die Länge des Medians des rechtwinkligen Dreiecks ABC, das der Ecke B entspricht, wird vollständig durch die Hälfte der Hypotenuse bestimmt. Erinnern Sie sich, dass der Median eines Dreiecks das Segment von einem der Eckpunkte zum Mittelpunkt der gegenüberliegenden Seite ist; in diesem Fall das BO-Segment.

Umschriebener Umfang

Eine andere Möglichkeit, den zweiten Satz von Thales zu sehen, ist durch einen Kreis, der in ein rechtes Dreieck umschrieben ist.

Im Allgemeinen besteht ein Kreis, der zu einem Polygon umschrieben ist, aus dem Umfang, der durch jeden seiner Eckpunkte verläuft, wann immer es möglich ist, ihn zu verfolgen.

Unter Verwendung des zweiten Satzes von Thales können wir bei einem rechtwinkligen Dreieck immer einen umschriebenen Umkreis mit einem Radius gleich der Hälfte der Hypotenuse und dem Umkreismittelpunkt (Mittelpunkt des Umfangs), der dem Mittelpunkt der Hypotenuse entspricht, konstruieren.

Anwendung

Eine sehr wichtige Anwendung des zweiten Satzes Solche und vielleicht die am meisten verwendet wird, ist die Tangenten zu einem bestimmten Umfang, durch einen äußeren Punkt P zu der (bekannten) zu finden.

Beachten Sie, dass bei einem Umfang (in der Abbildung unten blau eingezeichnet) und einem äußeren Punkt P zwei Linien vorhanden sind, die tangential zum Umfang verlaufen und P passieren. Seien T und T 'die Tangentenpunkte, r der Radius des Umfangs und Oder das Zentrum.

Es ist bekannt, dass das Segment, das von der Mitte eines Kreises zu einem Tangentialpunkt von ihm geht, senkrecht zu dieser Tangentenlinie ist. Dann ist der OTP-Winkel gerade.

Aus dem, was wir früher im ersten Satz von Thales und seinen verschiedenen Versionen sahen, sehen wir, dass es möglich ist, das OTP-Dreieck in einem anderen Umfang (in Rot) zu schreiben.

In analoger Weise wird erreicht, dass das OT'P-Dreieck innerhalb des gleichen vorhergehenden Umfangs eingeschrieben werden kann.

Für den zweiten Additionstheorem Solche erhalten wir das neue Kreisdurchmesser ist genau die Hypotenuse des Dreiecks OTP (die die Hypotenuse des Dreiecks OT'P gleich ist), und das Zentrum ist der Mittelpunkt dieser Hypotenuse.

Um den Mittelpunkt des neuen Umfangs zu berechnen, reicht es dann aus, den Mittelpunkt zwischen dem Mittelpunkt - etwa M - des Anfangsumfangs (den wir bereits kennen) und dem Punkt P (den wir auch kennen) zu berechnen. Dann ist der Radius der Abstand zwischen diesem Punkt M und P.

Mit dem Radius und der Mitte des roten Kreises können wir seine kartesische Gleichung finden, die daran erinnern, dass ist gegeben durch (x-h)² + (y-k)² = c², wobei c der Radius und der Punkt (h, k) der Mittelpunkt des Kreises ist.

Wenn wir nun die Gleichungen beider Umfänge kennen, können wir sie durch Lösung des durch diese gebildeten Gleichungssystems schneiden und so die Tangentenpunkte T und T 'erhalten. Schließlich, um die gewünschten Tangenten zu kennen, genügt es, die Gleichung der Geraden zu finden, die durch T und P sowie durch T 'und P verlaufen.

Beispiel

Betrachten Sie einen Umfang von Durchmesser AC, Zentrum O und Radius 1 cm. Sei B ein Punkt auf dem Umfang, so dass AB = AC ist. Wie viel misst AB?

Lösung

Nach dem zweiten Satz von Thales haben wir, dass das Dreieck ABC ein Rechteck ist und die Hypotenuse dem Durchmesser entspricht, der in diesem Fall 2 cm misst (der Radius ist 1 cm). Dann müssen wir nach dem Satz des Pythagoras:

Referenzen

1. Ana Lira, P.J. (2006). Geometrie und Trigonometrie. Zapopan, Jalisco: Schwellenausgaben.
2. Goodman, A. & Hirsch, L. (1996). Algebra und Trigonometrie mit analytischer Geometrie. Pearson Ausbildung.
3. Gutiérrez, Á. Á. (2004). Methodologie und Anwendungen der Mathematik in der E.S.O. Ministerium für Bildung.
4. IGER. (2014). Mathematik Zweites Semester Zacleu. Guatemala: IGER.
5. José Jiménez, L.J. (2006). Mathematik 2. Zapopan, Jalisco: Schwellenausgaben.
6. M., S. (1997). Trigonometrie und analytische Geometrie. Pearson Ausbildung.
7. Pérez, M. A. (2009). Eine Geschichte der Mathematik: Herausforderungen und Erfolge durch ihre Charaktere. Editorial Vision Bücher.
8. Viloria, N. & Leal, J. (2005). Flache analytische Geometrie. Venezolanischer Editorial C.